


Next: About this document ...
Tidal truncation of the viscous disk
Artymowicz & Lubow (1994) investigated the tidal/resonant truncation
of the accretion disks in eccentric binary systems and found that the
disk size becomes smaller in a system with larger
eccentricity. Following their formulation of the companion-disk
interaction, we study below the tidal truncation of the Be-star disk
in 4U0115+634.
In order to evaluate the tidal/resonant torque on the Be-star disk
exerted by the neutron star, we consider the binary potential in a
coordinate system
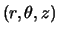 in which the origin is attached
to the Be star primary:
in which the origin is attached
to the Be star primary:
where  and
and  are masses of the Be and neutron stars,
respectively,
are masses of the Be and neutron stars,
respectively, 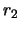 is the distance of the neutron star from the
primary, and
is the distance of the neutron star from the
primary, and 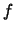 is the true anomaly of the neutron star. The third
term in the right hand side of Eq.(1) is the indirect
potential arised because the coordinate origin is at the primary.
is the true anomaly of the neutron star. The third
term in the right hand side of Eq.(1) is the indirect
potential arised because the coordinate origin is at the primary.
We expand the potential by a double series as
![\begin{displaymath}
\Phi (r, \theta, z)
= \sum_{m,l} \phi_{ml} \exp[i(m \theta - l \Omega_B t)],
\end{displaymath}](img10.gif) |
(2) |
where 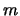 and
and 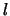 are the azimuthal and time-harmonic numbers,
respectively, and
are the azimuthal and time-harmonic numbers,
respectively, and
![$\Omega_B = [G(M_1+M_2)/a^3]^{1/2}$](img13.gif) is the mean
motion of the binary with semimajor axis
is the mean
motion of the binary with semimajor axis 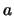 . The pattern speed of
each potential component is given by
. The pattern speed of
each potential component is given by
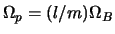 .
.
Inverting Eq.(2) and denoting the angle 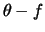 as
as
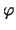 , we have
, we have
where 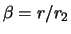 and
and 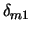 is the Kronecker delta
function.
is the Kronecker delta
function.
For each potential component 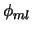 , there can be outer and inner
Lindblad resonances at radii where
, there can be outer and inner
Lindblad resonances at radii where
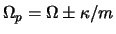 and
a corotation resonance at the radius where
and
a corotation resonance at the radius where
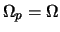 . Here,
. Here,
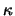 is the epicyclic frequency, and here and hereafter the upper
and lower signs correspond to the outer Lindblad resonance (OLR) and
inner Lindblad resonance (ILR), respectively. The radii of these
resonances are given by
is the epicyclic frequency, and here and hereafter the upper
and lower signs correspond to the outer Lindblad resonance (OLR) and
inner Lindblad resonance (ILR), respectively. The radii of these
resonances are given by
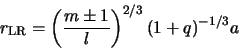 |
(4) |
and
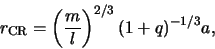 |
(5) |
where  .
.
For near Keplerian disks, where
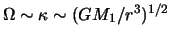 ,
the Goldreich & Tremaine (1979, 1980)'s standard formula for torques
,
the Goldreich & Tremaine (1979, 1980)'s standard formula for torques
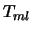 at the outer Lindblad resonance (OLR) and inner Lindblad
resonance (ILR) is reduced to
at the outer Lindblad resonance (OLR) and inner Lindblad
resonance (ILR) is reduced to
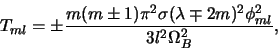 |
(6) |
where 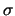 is the surface density of the disk at the resonance
radius and
is the surface density of the disk at the resonance
radius and
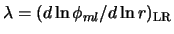 . Similarly,
torques at the corotation resonance (CR) is written as
. Similarly,
torques at the corotation resonance (CR) is written as
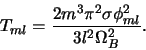 |
(7) |
Note that angular mommentum is removed from the disk at the ILRs,
whereas it is added to the disk at the OLRs and CRs.
In near Keplerian disks, the viscous torque formula derived by Lin &
Papaloizou (1986) is written as
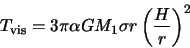 |
(8) |
[see also Artymowicz & Lubow (1994)], where 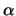 is the
Shakura-Sunyaev viscosity parameter and
is the
Shakura-Sunyaev viscosity parameter and 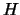 is the vertical
scale-height of the disk given by
is the vertical
scale-height of the disk given by
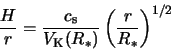 |
(9) |
for the isothermal disk.
Here,  is the sound speed and
is the sound speed and
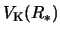 is the Keplerian velocity at the stellar surface.
In the systems we will discuss later,
is the Keplerian velocity at the stellar surface.
In the systems we will discuss later,
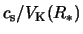 ranges
ranges
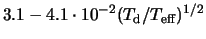 , where
, where
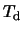 and
and 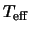 are the disk and stellar temperatures,
respectively. In what follows, we adopt
are the disk and stellar temperatures,
respectively. In what follows, we adopt
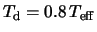 .
.
The disk is truncated if the viscous torque is
smaller than the resonant torque. The criterion for the disk
truncation at a given resonance radius is, in general, written as
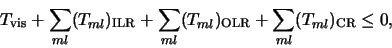 |
(10) |
where the summation is taken over all combination of 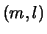 which
gives the same resonance radius. Actually,
criterion (10) is determined only by the viscous
torque and the torques from the ILRs of several lowest-order potential
components, because the torques from the ILRs dominate those from the
OLR and CR in circumstellar disks
and high-order potential components little contribute to the total
torque, even if the eccentricity of the orbit
which
gives the same resonance radius. Actually,
criterion (10) is determined only by the viscous
torque and the torques from the ILRs of several lowest-order potential
components, because the torques from the ILRs dominate those from the
OLR and CR in circumstellar disks
and high-order potential components little contribute to the total
torque, even if the eccentricity of the orbit 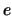 is not small
(Goldreich & Tremaine 1980; Artymowicz & Lubow 1994).
is not small
(Goldreich & Tremaine 1980; Artymowicz & Lubow 1994).
Note that the criterian (10) at a given resonance is
met for 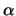 smaller than a critical value
smaller than a critical value
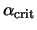 .
.



Next: About this document ...
Atsuo Okazaki
2001-01-05
![]() in which the origin is attached
to the Be star primary:
in which the origin is attached
to the Be star primary:
![]() as
as
![]() , we have
, we have
![]() , there can be outer and inner
Lindblad resonances at radii where
, there can be outer and inner
Lindblad resonances at radii where
![]() and
a corotation resonance at the radius where
and
a corotation resonance at the radius where
![]() . Here,
. Here,
![]() is the epicyclic frequency, and here and hereafter the upper
and lower signs correspond to the outer Lindblad resonance (OLR) and
inner Lindblad resonance (ILR), respectively. The radii of these
resonances are given by
is the epicyclic frequency, and here and hereafter the upper
and lower signs correspond to the outer Lindblad resonance (OLR) and
inner Lindblad resonance (ILR), respectively. The radii of these
resonances are given by
![]() ,
the Goldreich & Tremaine (1979, 1980)'s standard formula for torques
,
the Goldreich & Tremaine (1979, 1980)'s standard formula for torques
![]() at the outer Lindblad resonance (OLR) and inner Lindblad
resonance (ILR) is reduced to
at the outer Lindblad resonance (OLR) and inner Lindblad
resonance (ILR) is reduced to
![]() smaller than a critical value
smaller than a critical value
![]() .
.